This note is a short summary of my IEEE Transactions on Computers journal paper and was originally written to appear on the Graphcore blog.
The Graphcore IPU contains a novel pseudorandom number generator (PRNG) that was designed to produce high-quality statistical randomness, whist also being cheap to implement in hardware. Having an efficient hardware RNG means randomness can be used frequently: the IPUs generator can produce 64-bits of unique randomness from all of its 1,216 tiles every clock cycle. This, for example, makes it possible to perform on-the-fly stochastic rounding of low-precision floating-point numbers.
We needed a new PRNG because typical state-of-the-art generators are designed
to be performant when run as software routines, but operations that are cheap
to execute on a processor may not be cheap to implement in hardware as is the
case for multiplication or division. Our generator xoroshiro128aox is based
on Sebastiano Vigna’s xoroshiro128
linear-feedback shift register (LFSR), which is attractive because it uses 128
bits of state and is cheap to implement in hardware. The LFSR operates by
performing XOR and fixed-distance shift and rotate operations on the state.
Following Vigna’s approach of adding a function to ‘scramble’ the LFSR state,
we have devised a function consisting of AND, OR and XOR operations (called AOX
for short). An C implementation of xoroshiro128aox is as follows:
uint64_t s0, s1; // State vectors
uint64_t rotl(uint64_t x, int k) {
return (x << k) | (x >> (64 - k));
}
uint64_t next(void) {
uint64_t sx = s0 ^ s1;
// Calculate the result, the 'AOX' step.
uint64_t sa = s0 & s1;
uint64_t res = sx ^ (rotl(sa, 1) | rotl(sa, 2));
// xoroshiro128 state update
s0 = rotl(s0, 55) ^ sx ^ (sx << 14);
s1 = rotl(sx, 36);
return res;
}
To determine that this new PRNG provides a good source of randomness, we took the conventional approach of subjecting the generator to batteries of statistical tests, that aim to detect correlations over large portions of the generator’s output. Given that any PRNG is inherently non-random because they produce numbers according to a fixed sequence, statistical testing is only as good as the tests that they run, and their performance can only be judged on their ability to distinguish existing good generators from bad ones. Indeed, a novel statistical test could immediately raise the bar for all PRNGs.
Within the field of PRNG design, TestU01’s BigCrush battery is accepted as the gold-standard statistical test, however it is not always clear exactly what methodology has been used to obtain a pass/fail result. In particular, the choice of initial state (the seed) is important because different parts of a sequence may have different properties, and TestU01 has known biases in the way it uses bits from a generator’s output. To mitigate these issues, we run every generator from 100 unique seeds and supply six permutations of the output bits. And as well as running TestU01, we also run PractRand and Gjrand with the same 100 seeds, which are the two other most well-regarded test sets. This gives us a comprehensive testing methodology that goes beyond the typical level of analysis.
To provide a point of comparison, we include the following PRNGs:
-
32-bit Mersenne Twister,
mt32, since it is one of the most widely used software PRNGs (although it has 19,937 bits of state!). -
xoroshiro128+, which is Vigna’s closest variant ofxoroshiro128, using 64-bit addition to scramble 128-bit LFSR states.
And to represent the current state-of-the-art 128-bit generators, we include:
-
philox4x32-10, a counter-based generator whose transition between states is a 128-bit increment and output scrambling function is 10 rounds of 32-bit multiplications and XORs. -
pcg64, a linear-congruential generator (LCG) that uses multiplication and addition by 128-bit constants for the state-transition function, and XOR and variable rotation operations to produce outputs.
The table below summarises the TestU01 BigCrush results, where the six output columns correspond to different permutations of the generators bits (eg 1 is unchanged, 2 is swapping the most and least significant 32 bits) and the numbers are total failures. Since a true random number generator has a probability of failing, the expected number of failures can be calculated. BigCrush runs 160 individual tests (and consumes approximately 1 TB of random data), so in this case the expected number is 32. A generator is considered to fail only when it fails on the same test over all seeds, which can be seen in the entries highlighted in red. The Mersenne Twister consistently fails, whereas xoroshiro128+ fails on a particular output permutation where the lower 32 bits are discarded (this is a known deficiency of the generator).
| Generator | Output 1 | Output 2 | Output 3 | Output 4 | Output 5 | Output 6 | Total failures |
|---|---|---|---|---|---|---|---|
mt32 |
236 | 237 | 233 | 238 | 246 | 237 | 1427 |
pcg64 |
34 | 30 | 38 | 37 | 38 | 27 | 204 |
philox4x32-10 |
33 | 32 | 32 | 32 | 28 | 38 | 195 |
xoroshiro128+ |
33 | 29 | 28 | 40 | 353 | 42 | 525 |
xoroshiro128aox |
31 | 32 | 41 | 30 | 44 | 32 | 210 |
The table below summarises the Gjrand results, which just runs 13 tests and by default consumes approximately 10 TB of data. Unlike BigCrush and TestU01, xoroshiro128aox fails Gjrand on both versions of its z9 test, which looks for dependencies in the Hamming Weight of successive outputs. Although BigCrush and PractRand include similar tests that analyse Hamming Weight dependencies, they do not detect correlations. What this shows is that the scrambling of the xoroshiro128 LFSR’s state serves to hide correlations due to the linear operations only to an extent, and a particular test will be sensitive enough to detect them. Given that BigCrush and PractRand did not, xoroshiro128aox represents a significant improvement over xoroshiro128+, whilst still being cheap to implement in hardware as we show in the next section.
| Generator | Total failures |
|---|---|
mt32 |
107 |
pcg64 |
15 |
philox4x32-10 |
7 |
xoroshiro128+ |
210 |
xoroshiro128aox |
205 |
To demonstrate that xoroshiro128aox is indeed cheap to implement in hardware, we compare physical implementations of the generators (excluding Mersenne Twister because of its considerable state size) after they have been fully synthesised and placed and routed using Graphcore’s 7 nm cell library and a target clock period of 1 GHz. The table below summarises the results.
| Generator | Total cells (state update) | Logic depth (state update) | Total cells (output) | Logic depth (output) | Total cells |
|---|---|---|---|---|---|
xoroshiro128aox |
331 | 4 | 353 | 4 | 684 |
xoroshiro128+ |
331 | 3 | 906 | 13 | 1237 |
pcg64 |
9564 | 26 | 658 | 7 | 10222 |
philox4x32-10 |
1003 | 13 | 29553 | 89 | 30556 |
Key takeaways from these results are:
-
That AOX is approximately one third of the cost of a full 64-bit addition and the cheapest option overall by a factor of two.
-
For
pcg64the cost is dominated by the 128-bit arithmetic for its state update. -
For
philox4x32-10the cost is dominated by the output function composed of 10 stages of 32-bit arithmetic.
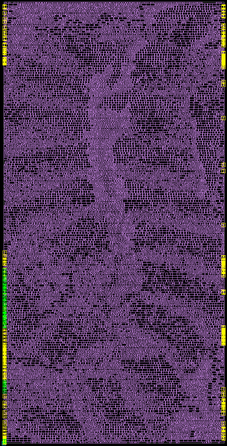
The following are illustrations of the four PRNG circuit floorplans, which make
clear the differences in implementation complexity (left to right:
xoroshiro128aox, xoroshiro128+, pcg64, philox4x32-10):
And scaled to relative sizes:
Summary
This note has provided an overview of the methodology and results of the
analysis we conducted into the statistical quality of our novel PRNG
xoroshiro128aox. This has established that our generator mitigates known
existing weaknesses of xoroshiro128+ on which it is based, and delivers
comparable levels of statistical quality on the gold-standard BigCrush test set
as two contemporary fast PRNGs : pcg64 and philox4x32-10. Extending
testing by using PractRand and Gjrand, we do eventually find that a weakness is
detectable by Gjrand. Since this is not systematic across the test suites, as
we have seen for the Mersenne Twister, we can consider xoroshiro128aox to
provide an excellent tradeoff between quality and implementation cost in hardware.
Full details of the investigation can be found in the preprint paper on arXiv, and the source code for the experiments on GitHub.